얼거스 개발 일지

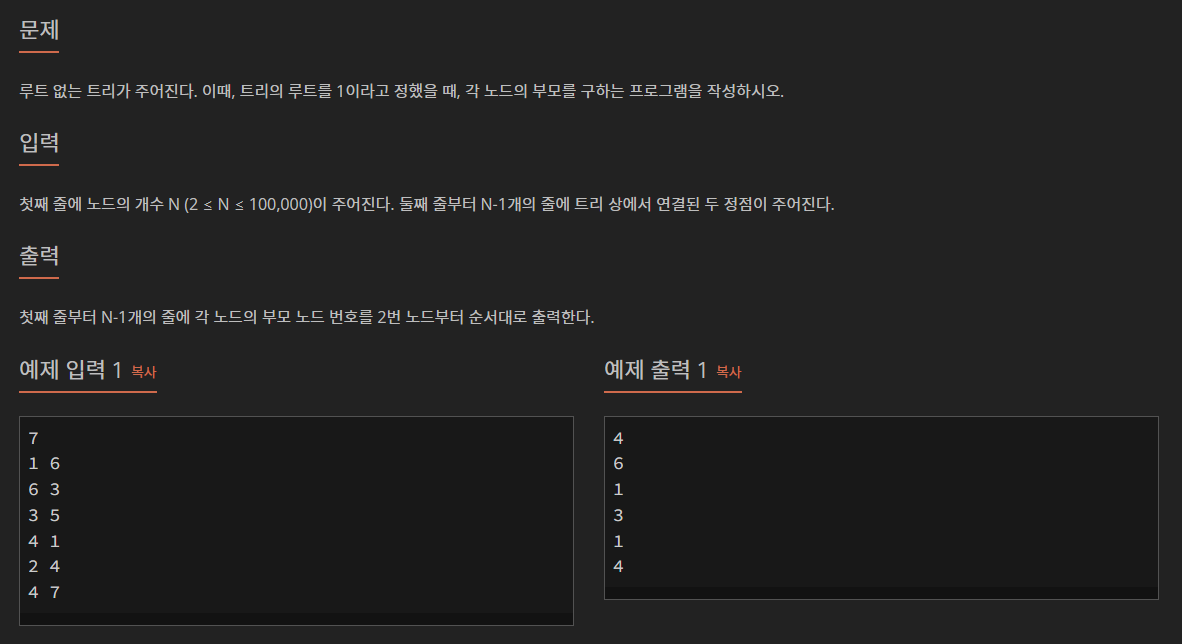
내 코드

public class Test17 {
    public void main() {
        try (BufferedReader br = new BufferedReader(new InputStreamReader(System.in))) {
            int n = Integer.parseInt(br.readLine());

            // 트리 만들기
            ArrayList<ArrayList<Integer>> tree = new ArrayList<>();
            for (int i = 0; i <= n; i++) {
                tree.add(new ArrayList<>());
            }
            for (int i = 0; i < n - 1; i++) {
                StringTokenizer st = new StringTokenizer(br.readLine());
                int l = Integer.parseInt(st.nextToken());
                int r = Integer.parseInt(st.nextToken());

                tree.get(l).add(r);
                tree.get(r).add(l);
            }

            // 부모 찾기 BFS
            int[] p = new int[n + 1];
            Queue<Integer> q = new LinkedList<>();
            q.offer(1);
            while (! q.isEmpty()) {
                int now = q.poll();

                ArrayList<Integer> child = tree.get(now);
                for (int i = 0;  i < child.size(); i++) {
                    int cur = child.get(i);
                    if (p[cur] != 0) continue;

                    p[cur] = now;
                    q.offer(cur);
                }
            }

            for (int i = 2; i < p.length; i++) {
                System.out.println(p[i]);
            }
        } catch (Exception e) {
            System.out.println("err 😭");
            e.printStackTrace();
        }
    }

다른 사람 코드 1

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
int[] parent = new int[n + 1];
ArrayList<ArrayList<Integer>> list = new ArrayList<>();

// list 초기화
for (int i = 0; i <= n; i++) {
	list.add(new ArrayList<>());
}

// 데이터(노드) 삽입
for (int i = 1; i < n; i++) {
	StringTokenizer st = new StringTokenizer(br.readLine());
    int node1 = Integer.parseInt(st.nextToken());
    int node2 = Integer.parseInt(st.nextToken());

	list.get(node1).add(node2);
	list.get(node2).add(node1);
}

// 부모 찾기 : Q 이용
// 각 노드 큐에 저장
Queue<Integer> q = new LinkedList<>();
q.offer(1); // root 입력
while (!q.isEmpty()) {
	int now = q.poll();

	for (int child: list.get(now)) {

		if (parent[child] != 0) continue;

		parent[child] = now;
        q.offer(child);
	}
}

// 부모 출력
for (int i = 2; i <= n; i++) {
	System.out.println(parent[i]);
}

다른 사람 코드2

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        Tree tree = new Tree(n);
        for (int i = 1; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine(), " ");
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            tree.addEdge(a, b);
        }

        tree.bfs(1);
        tree.printParents();
    }
}

class Tree {
    private ArrayList<ArrayList<Integer>> list;
    private int[] parents;
    private int size;

    public Tree(int n) {
        size = n;
        list = new ArrayList<>();
        parents = new int[n + 1];

        for (int i = 0; i <= n + 1; i++) {
            list.add(new ArrayList<>());
        }
    }

    public void addEdge(int a, int b) {
        list.get(a).add(b);
        list.get(b).add(a);
    }

    public void bfs(int start) {
        Queue<Integer> queue = new LinkedList<>();
        boolean[] visited = new boolean[size + 1];
        visited[start] = true;
        queue.add(start);

        while (!queue.isEmpty()) {
            int currentNode = queue.poll();

            for (int nextNode : list.get(currentNode)) {
                if (!visited[nextNode]) {
                    visited[nextNode] = true;
                    parents[nextNode] = currentNode;
                    queue.add(nextNode);
                }
            }
        }
    }

    public void printParents() {
        for (int i = 2; i <= size; i++) {
            System.out.println(parents[i]);
        }
    }
}

트리는 그래프의 한 종류로서 특정한 제약 조건을 충족하는 계층적인 구조를 가지고 있다. 루트 노드가 있으면 트리, 루트 노드가 없으면 그래프라고 볼 수도 있다. 어려웡 🙄 트리와 그래프. BFS, DFS
좀 오래 봐야할 느낌이다 🤔

BFS 너비 우선 탐색 알고리즘

시작 노드로부터 가장 가까운 노드 들을 먼저 탐색 한 후, 더 멀리 떨어져 있는 노드들을 차례대로 탐색하는 방식이다.

자료구조인 큐를 활용하며 , FIFO 원칙을 따른다.

BFS 알고리즘 수행 과정

1. 시작 노드를 큐에 넣고, 방문 처리를 한다.
2. 큐에서 노드를 꺼내어, 그 노드의 인접 노드들 중 아직 방문하지 않은 노드를 모두 큐에 넣고 방문 처리를 한다.
3. 큐가 빌때까지 2번을 반복한다.

BFS 알고리즘의 특징

1. 시작 노드에서 다른 노드까지의 최단 경로를 찾을 수 있다. 각 단계마다 가장 가까운 노드부터 탐색하기 때문이다.
2. 큐를 사용하여 탐색 순서를 관리한다. 이것은 DFS 알고리즘과 구분되는 점이다. DFS는 스택이나 재귀를 사용!
3. 그래프의 모든 노드를 방문할 수 있다. 이것은 완전 탐색 알고리즘으로 사용될수 있음을 뜻한다.

---

다시 풀어본 날 : 23.03.30 _ 04.01 _ 04.08 _ 04.09 실패 : 23.03.31 _ 04.02🤯

아오 어려웡 😭

04.08 _ 몇번 더 풀어봐야됨 😔 04.09 _ 드디어 막힘없이 한번에 풀긴 풀었는데 아직도 어렵다;; 이 문제는 익숙해질때까지 풀어보는걸로~~